Judging the Southeast Region

Pool Table was one of our tougher, E/F problems. There were two parts to the problem – figuring out that distance, and making sure you didn’t hit the target ball too soon.

Here’s the Judge Input, the Judge Output, the main Solving Program, another java solution, and one in C++.

Take a look in the Spoiler for solution ideas.

[spoiler]
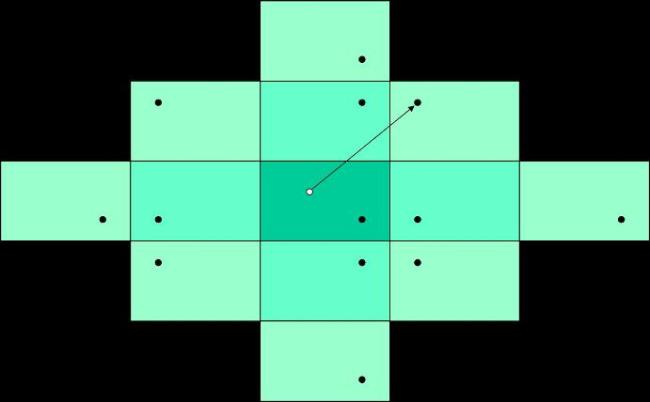
For the first part, finding the distance, it’s easier to not try to compute reflections, but rather to set up a coordinate system of reflected pool tables. Let dx and dy be a number of pool tables over, and up. If n is the desired number of bounces, then look at all reflections where |dx|+|dy|=n.

For example, if n=2 bounces, instead of this:

See it as this:

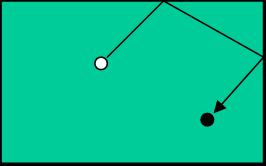
Then, look at all reflections where |dx|+|dy|=n (for our example of n=2, they’re the lightest colored ones in the example above), and just calculate the straight linear distance between the cue ball and the reflection of the target ball. Be careful about the position of the target ball in the reflection!

Then, the second part of the problem is to make sure that there are no reflections of the target ball that get in the way – that is, no chance of hitting the target ball too soon. You’ve got to check that no reflection of the target ball (including the original!) is collinear with the cue ball and the reflection you’re trying to hit AND between them.

Here’s a case that caught a few teams: consider a large table, with the cue at (1,1) and the target at (2,2), with n=2 bounces. The correct answer is to shoot at the corner at (0,0), and have the cue bounce straight back to the target. Several teams failed this particular test. It’s because, in checking to see if an earlier version of the target blocked the shot, they only checked collinearity, not betweenness. Here, the original target ball is collinear with the cue and the reflected target, but it is not between them!
[/spoiler]