Judging the Southeast Region

We considered this problem an E/F, World-Finals level of difficulty. There were 3 correct solutions – on only 7 submissions, and the first came only 65 minutes into the contest. It had the highest solution percentage of any problem outside of the two A/Bs (Knitting and Minesweeper). That means that few teams knew how to solve it, and few tried, but those who knew it, knew it well, and got it quickly and accurately.

Take a look at the Judge Input, the Judge Output, the main Solving Program, and another java solution.

A solution is in the spoiler.

[spoiler]
The key to understanding this solution is to see a column of the mosaic as a bitmap – with the bit set (=1) if there’s a tile there, and unset (=0) if not. Since there are at most 10 rows, that gives us 1024 possible bitmaps, which is manageable.

Try to build a Mosaic, column by column. Since the pieces are 2×2, you can’t fill a column without leaving some residue in the next column. So, you need to figure out, for any bitmap j representing a residue from the last column, how many ways can we fill this column and leave a residue of bitmap k in the next column? The following picture illustrates one way of filling 1001101001 (617) and ending up with 1111011110 (990).

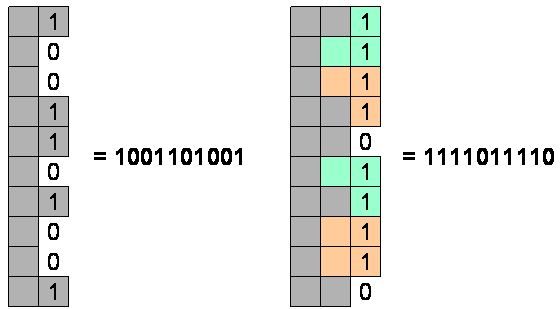
Here’s an interesting thing – that depends only on the number of rows. So, you can compute all of that a priori, before you start reading the data, rather than doing it over and over for each data set. A recursive algorithm will do the trick.

Once you’ve got that computed, then for each input, you need to fill the columns so that you start with a bitmap of 0 (on the edge, no residue), go through m columns, and end up with a bitmap of 0 (no residue – nothing hanging off the edge of the mosaic)

     
// Assume n rows and m columns.
// Let p be the number of bitmaps if there are n rows.
// So, p = 2^n, or 1<<n
int p = 1<<n;
       
// Let next[k] be the number of ways of achieving bitmap k
// on the next column
int next[] = new int[p];

// We'll start at the very beginning (a very good place to start)
// with one bitmap of 0, and no others.
next[0] = 1;

// Go through all of the columns
for( int i=0; i<m; i++ )
{
    // Swap current and next - last iterations' next[]
    // is this iteration's current[]
    int temp[] = current;
    current = next;
    next = temp;
            	
    // Start afresh
    Arrays.fill( next, 0 );
            	
    // Go through all possible bitmaps.
    for( int j=0; j<p; j++ ) if( current[j]>0 ) for( int k=0; k<p; k++  )
    {
        // Assume that ways[n][j][k] is the number of ways of getting from 
        // bitmap j to bitmap k if there are n rows. (In the actual code, a linked list 
        // is used for efficiency, since this matrix will be sparse.)
        //
        // If there are current[j] ways of getting to bitmap j on the current column,
        // and ways[n][j][k] ways of getting from there to bitmap k, then we've
        // just found current[j]*ways[n][j][k] more ways of getting to bitmap k
        // on the next column. So, add them in.
        next[k] += current[j] * ways[n][j][k];

        // Mod to keep the numbers manageable.
        next[k] %= 1000000;
    }
}

// We're done! How many ways were there of achieving bitmap 0
// on the last iteration - that is, we nicely filled in the mosaic with
// nothing hanging over?
System.out.println( next[0] );

[/spoiler]