Judging the Southeast Region

Here it is – the 2013 UChicago Invitational problem set. You can download the text from here.

A Russian contest is going to use this problem set in about a week, so we can’t post the data to the public just yet. I’ll post the usual problem breakdown in about a week, but for now, here’s the problem set & data for the UChicago 2013 Invitational contest. The data is encrypted and password protected, so that only participants can see it.

Problem set: UChicago Invitational 2012 Problem Set

Data: data

Here it is – the 2012 Division II problem set. You can download the text from here.

Here it is – the 2012 Division I problem set. You can download the text from here.

Here it is – the problem set. You can download the text from here.

Here is a video of a webcast of the Chief Judge (me) discussing each of the problems in the 2011 problem set. The original lecture was given at Georgia Tech on Thursday, 11 November. The video is about 90 minutes long. The real content starts at about the 2 minute mark.

[flv:http://vanb.org/ser2011/vanb_ser2011_lecture.flv X 640 480]

In the problem statement for Vive la Difference, we make the claim that if all four numbers are less than 2^n, then it will converge in no more than 3n steps. This PowerPoint presentation outlines a proof.

Here it is – the 2011 problem set. You can download the text from here.

sundaydrive.java

Here’s the Call for Problems that was recently sent out to all SER coaches and Problem Selection Committee members:

Summer is upon us, World Finals is over, so it’s time to start thinking, just a little bit, about the Southeast USA Regional Programming Contest. It’ll be a little bit earlier this year, on Saturday, 29 October. So, spend your summer dreaming up programming problems! Also, we’re looking for people to serve on the Problem Selection Committee. Putting together the problem set for SER is an intense, rewarding process. If you’re interested, send me an e-mail (at vanb@biltmorecomm.com).

As usual, the Problem Selection Committee will be responsible for putting the problem set together. The PSC will also be responsible for judging, so problem providers won’t have to judge. Because of this, you can provide a problem, and also coach your team, and attend the contest with them at your chosen site. Anyone can submit a problem for consideration – however, although a problem submitter can also act as a coach, they cannot be a contestant, whether or not their problem is chosen for the set. In other words, if a student submits a problem, they are ineligible to compete.

Candidate problems should be e-mailed to me (at vanb@biltmorecomm.com). A statement of the problem is all that’s necessary, either in text or in MS Word format (right in the e-mail is fine). If you wish to include a solving program and/or test data, that’s very, very helpful, but not necessary. If you have a rough idea and want to talk about it, feel free to e-mail it to me, and I’ll be happy to work with you.

Problems should be sent by Friday, 9 September to be eligible for consideration. That’s the Friday after Labor Day. I’ll remind you again, but I’m sending out the call for problems early, to get you thinking!

Below you will find an excerpt from the Call for Problems issued from World Finals this year. It’s a good set of guidelines for candidate problems. If you are thinking of submitting a candidate problem for Southeast Regionals, you should read through it. I will add a couple of constraints of my own:

1. The problem should be original. It should not be a restatement of a problem that has been used previously in the Southeast USA, or any other ICPC regional, World Finals, or other contest environment such as TopCoder or Google CodeJam. It also should not come from a book, such as “Programming Challenges.” If it has its own Wikipedia page, then it’s too well-known.
2. The output for any given input should be unique. Try to add constraints to your problem so that there is exactly one answer for each input case.

Don’t forget about the blog to talk about judging at our contest. It’s at:

http://serjudging.vanb.org

Feel free to drop by and give suggestions – however, do NOT post candidate problems on this site. It is open to everyone, including students. Any problem posted on the site cannot be used in the contest.

————- Some excerpts from the World Finals call for problems: ————-

Problem Statements

1. Each problem must be unambiguously described in English.
2. All problems must require input.
3. Unless the core of the problem is input/output related, the formats chosen for input data and the displayed results should be relatively simple. Still, the format of the input data and the appearance of the expected displayed results must be described in suitable detail.
4. Multiple data sets testing different cases are appropriate; make the problem statement include iterative data sets as input to avoid using separate input files.
5. Anticipate questions about special cases. Where appropriate, explicitly state that certain special cases will not appear in the input data. It is not necessary to specifically identify the special cases that will appear.
6. Indicate the precision that is required for real results.
7. Contestants must write solutions for problems in a short time. While very simple problems are not appropriate, neither are problems that require a great deal of code; a few hundred lines of Java or C should be an upper limit on what can be expected in a solution.
8. The program and chosen test data should not require excessive execution time. Contestants’ solutions may be less efficient than yours and so a generous margin is allowed for execution. If your test data requires the program to execute for a long time, then incorrect student solutions (e.g., those with infinite loops) will take an excessively long time to judge. We would like to avoid those situations.
9. The problem description (excluding sample input/output) should generally require at most one page.

Submission of Problems, Solutions, and Test Data

1. Use electronic mail and send all files as either MS Word document, or flat ASCII.
2. Do not put your name in documents, or the body of e-mails, containing the problem statement, solution, or test data. This will simplify the transformation from your form to the one used for ranking.
3. Be discreet about problem statements and solutions. It is not appropriate to discuss problems with people not involved with the contest.

Here it is – the 2010 problem set. You can download the text from here.

The Southeast USA Regional Programming Contest will be held on Saturday 6 November this year, and I will once again be Chief Judge.

As usual, the Problem Selection Committee will be responsible for putting the problem set together. The PSC will also be responsible for judging, so problem providers won’t have to judge. Because of this, you can provide a problem, and also coach your team, and attend the contest with them at your chosen site. Anyone can submit a problem for consideration – however, although a problem submitter can also act as a coach, they cannot be a contestant, whether or not their problem is chosen for the set. In other words, if a student submits a problem, they are ineligible to compete.

Candidate problems should be e-mailed to me (at vanb@vanb.org). A statement of the problem is all that’s necessary, either in text or in MS Word format (right in the e-mail is fine). If you wish to include a solving program and/or test data, that’s very, very helpful, but not necessary. If you have a rough idea and want to talk about it, feel free to e-mail it to me, and I’ll be happy to work with you.

Problems should be sent by 13 September to be eligible for consideration. I’ll remind you again, but I’m sending out the call for problems early, to get you thinking!

Below you will find an excerpt from the Call for Problems issued from World Finals this year. It’s a good set of guidelines for candidate problems. If you are thinking of submitting a candidate problem for Southeast Regionals, you should read through it. I will add a couple of constraints of my own:

1. The problem should be original. It should not be a restatement of a problem that has been used previously in the Southeast USA, or any other ICPC regional, World Finals, or other contest environment such as TopCoder or Google CodeJam. It also should not come from a book, such as “Programming Challenges.” If it has its own Wikipedia page, then it’s too well-known.
2. The output for any given input should be unique. Try to add constraints to your problem so that there is exactly one answer for each input case.

Based on suggestions from last year’s regional contest, I have started a blog to talk about judging at our contest. It’s at:

http://serjudging.vanb.org

Feel free to drop by and give suggestions – however, do NOT post candidate problems on this site. It is open to everyone, including students. Any problem posted on the site cannot be used in the contest.

————- Some excerpts from the World Finals call for problems: ————-

Problem Statements

1. Each problem must be unambiguously described in English.
2. All problems must require input.
3. Unless the core of the problem is input/output related, the formats chosen for input data and the displayed results should be relatively simple. Still, the format of the input data and the appearance of the expected displayed results must be described in suitable detail.
4. Multiple data sets testing different cases are appropriate; make the problem statement include iterative data sets as input to avoid using separate input files.
5. Anticipate questions about special cases. Where appropriate, explicitly state that certain special cases will not appear in the input data. It is not necessary to specifically identify the special cases that will appear.
6. Indicate the precision that is required for real results.
7. Contestants must write solutions for problems in a short time. While very simple problems are not appropriate, neither are problems that require a great deal of code; a few hundred lines of Java or C should be an upper
   limit on what can be expected in a solution.
8. The program and chosen test data should not require excessive execution time. Contestants’ solutions may be less efficient than yours and so a generous margin is allowed for execution. If your test data requires the program to execute for a long time, then incorrect student solutions (e.g., those with infinite loops) will take an excessively long time to judge. We would like to avoid those situations.
9. The problem description (excluding sample input/output) should generally require at most one page.

Submission of Problems, Solutions, and Test Data

1. Use electronic mail and send all files as either MS Word documents, or flat ASCII.
2. Do not put your name in documents, or the body of e-mails, containing the problem statement, solution, or test data. This will simplify the transformation from your form to the one used for ranking.
3. Be discreet about problem statements and solutions. It is not appropriate to discuss problems with people not involved with the contest.

We considered this problem an E/F, World-Finals level of difficulty. There were 3 correct solutions – on only 7 submissions, and the first came only 65 minutes into the contest. It had the highest solution percentage of any problem outside of the two A/Bs (Knitting and Minesweeper). That means that few teams knew how to solve it, and few tried, but those who knew it, knew it well, and got it quickly and accurately.

Take a look at the Judge Input, the Judge Output, the main Solving Program, and another java solution.

A solution is in the spoiler.

[spoiler]
The key to understanding this solution is to see a column of the mosaic as a bitmap – with the bit set (=1) if there’s a tile there, and unset (=0) if not. Since there are at most 10 rows, that gives us 1024 possible bitmaps, which is manageable.

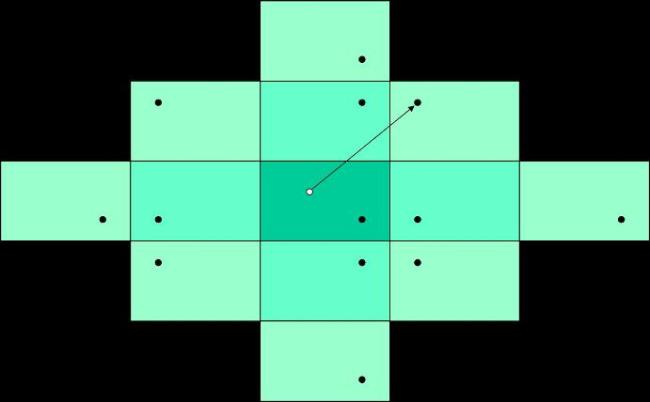
Try to build a Mosaic, column by column. Since the pieces are 2×2, you can’t fill a column without leaving some residue in the next column. So, you need to figure out, for any bitmap j representing a residue from the last column, how many ways can we fill this column and leave a residue of bitmap k in the next column? The following picture illustrates one way of filling 1001101001 (617) and ending up with 1111011110 (990).

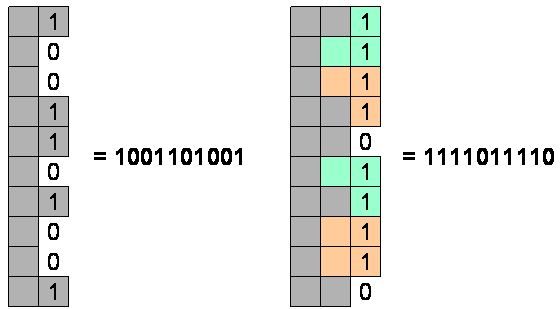
Here’s an interesting thing – that depends only on the number of rows. So, you can compute all of that a priori, before you start reading the data, rather than doing it over and over for each data set. A recursive algorithm will do the trick.

Once you’ve got that computed, then for each input, you need to fill the columns so that you start with a bitmap of 0 (on the edge, no residue), go through m columns, and end up with a bitmap of 0 (no residue – nothing hanging off the edge of the mosaic)

     
// Assume n rows and m columns.
// Let p be the number of bitmaps if there are n rows.
// So, p = 2^n, or 1<<n
int p = 1<<n;
       
// Let next[k] be the number of ways of achieving bitmap k
// on the next column
int next[] = new int[p];

// We'll start at the very beginning (a very good place to start)
// with one bitmap of 0, and no others.
next[0] = 1;

// Go through all of the columns
for( int i=0; i<m; i++ )
{
    // Swap current and next - last iterations' next[]
    // is this iteration's current[]
    int temp[] = current;
    current = next;
    next = temp;
            	
    // Start afresh
    Arrays.fill( next, 0 );
            	
    // Go through all possible bitmaps.
    for( int j=0; j<p; j++ ) if( current[j]>0 ) for( int k=0; k<p; k++  )
    {
        // Assume that ways[n][j][k] is the number of ways of getting from 
        // bitmap j to bitmap k if there are n rows. (In the actual code, a linked list 
        // is used for efficiency, since this matrix will be sparse.)
        //
        // If there are current[j] ways of getting to bitmap j on the current column,
        // and ways[n][j][k] ways of getting from there to bitmap k, then we've
        // just found current[j]*ways[n][j][k] more ways of getting to bitmap k
        // on the next column. So, add them in.
        next[k] += current[j] * ways[n][j][k];

        // Mod to keep the numbers manageable.
        next[k] %= 1000000;
    }
}

// We're done! How many ways were there of achieving bitmap 0
// on the last iteration - that is, we nicely filled in the mosaic with
// nothing hanging over?
System.out.println( next[0] );

[/spoiler]

We had wanted this problem to be a Dynamic Programming problem, and early versions of it had large input limits that would force DP. However, other constraints caused us to put limits on it, making it solvable by other means. It was in our “second wave” of problems. The “first wave” was Knitting and Minesweeper – every team that solved one or two problems solved one (or both) of those two. This problem and “Euclid” made up the second wave – every team that solved 3 or 4 solved both problems in the first wave, and then one or two from the second wave. Every team that solved more than 4 solved both problems in the first wave, and both problems in the second wave.

OK, here’s the Judge Input, the Judge Output, the main Solving Program, another java solution, one in C++, another in C++, and one using a different technique.

Look in the spoiler for not one, but two solution ideas!

[spoiler]
The original intent was for this problem to require Dynamic Programming. Create an array best[], where best[i] is the best you can do from here to the end if you stop at target point i. Clearly, best[i] can be computed pretty simply from best[i+1], best[i+2], and so on (best[i] = Minimum over k of [1+(the cost of skipping targets between i and i+k) + (the Euclidean distance between i and i+k) + best[i+k]]. ). So, start at the end, work back to the beginning, and best[0] is your answer.

The numbers were small enough, however, that a simple, best-first-search shortest path (aka Dijkstra’s Algorithm) would work. Define the “Distance” between two targets as 1 + (the Euclidean distance) + (the cost of skipping targets in between). Then, just run Dijkstra’s Algorithm and voila.

Note: in both cases, the “1+” is for the one second that the robot must stop on a target point.
[/spoiler]

Pool Table was one of our tougher, E/F problems. There were two parts to the problem – figuring out that distance, and making sure you didn’t hit the target ball too soon.

Here’s the Judge Input, the Judge Output, the main Solving Program, another java solution, and one in C++.

Take a look in the Spoiler for solution ideas.

[spoiler]
For the first part, finding the distance, it’s easier to not try to compute reflections, but rather to set up a coordinate system of reflected pool tables. Let dx and dy be a number of pool tables over, and up. If n is the desired number of bounces, then look at all reflections where |dx|+|dy|=n.

For example, if n=2 bounces, instead of this:

See it as this:

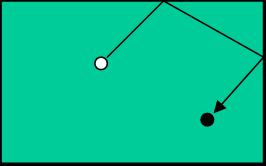
Then, look at all reflections where |dx|+|dy|=n (for our example of n=2, they’re the lightest colored ones in the example above), and just calculate the straight linear distance between the cue ball and the reflection of the target ball. Be careful about the position of the target ball in the reflection!

Then, the second part of the problem is to make sure that there are no reflections of the target ball that get in the way – that is, no chance of hitting the target ball too soon. You’ve got to check that no reflection of the target ball (including the original!) is collinear with the cue ball and the reflection you’re trying to hit AND between them.

Here’s a case that caught a few teams: consider a large table, with the cue at (1,1) and the target at (2,2), with n=2 bounces. The correct answer is to shoot at the corner at (0,0), and have the cue bounce straight back to the target. Several teams failed this particular test. It’s because, in checking to see if an earlier version of the target blocked the shot, they only checked collinearity, not betweenness. Here, the original target ball is collinear with the cue and the reflected target, but it is not between them!
[/spoiler]

This problem turned out to be harder than we expected. We rated it a C/D, yet only 2 teams managed to solve it, the first coming about three and a half hours into the contest. It’s really not a difficult algorithm, but it’s off the beaten path, and requires some thinking and some care.

Check out the Judge Input, the Judge Output, the main Solving Program, another java solution, and one in C++.

Look in the spoiler for a description of a solution.
[spoiler]
Use a Greedy algorithm. First, assume that the trees are laid out right next to each other, as tightly as possible. Then, find the positions of the smallest and largest trees – let’s say s and t – and then try to stretch the gap between s and s+1 as far as possible, then the gap between s+1 and s+2, then s+2 and s+3, all the way up to t-1 and t. Look at all pairs of trees that are adjacent height-wise (that the Ninjas would jump between) that span each of those gaps, to see how far the gaps can be stretched.

The only way the Greedy algorithm can fail is if stretching an early gap limits your options of stretching a later gap. I’m not going to go through a convoluted argument, but it’s true. It’s left as an exercise to the reader to confirm!
[/spoiler]

It’s just Minesweeper. Everyone knows Minesweeper. This problem was solved by more teams than any other.

Check out the Judge Input, the Judge Output, the main Solving Program, another solution, and another. There are also C++ solutions here and here.

[spoiler]
The algorithm is obvious – just do what the problem says. For every non-mine cell, look at the (up to) 8 cells around, and count the number of mines. So, the key to solving this problem is just to be careful about certain things.

• Don’t go off the edge of the board when you’re checking edge cells and corner cells
• For some, correctly convert an integer to a char (others just printed the int directly). In both C++ and Java, this will work: ch = (char)(x+’0′)
• Make sure your output spacing is correct.

[/spoiler]

Knitting was one of the two easiest problems in the set (Minesweeper is the other), and was solved by most teams.

Here’s the Judge Input, the Judge Output, the main Solving Program, another solution, and another.

There’s a pseudocode solution in the spoiler.
[spoiler]
The only real trick is to recognize that the numbers are so small that you don’t need fancy math. Just iterate through it.

    Input numberOfRows, firstRow, numberOfDeltas, deltas
    stitchesOnRow = firstRow
    total = 0;
    For i = 0 to numberOfRows-1
        total = total + stitchesOnRow
        stitchesOnRow = stitchesOnRow + deltas[i mod numberOfDeltas]
    End
    Print total

[/spoiler]

This was the hardest problem in the set. No team solved it, although several came close. Here’s one bit of trickyness that bit some teams – the problem states:

These time intervals may overlap. The union of all time intervals provides the complete set of times at which the guard is available.

If a guard says they’re available from 2:05 to 3:15, and also from 3:10 to 4:20, then they are available for the 3:00 to 3:30 time interval. Some teams did not perform this union correctly.

Here’s the Judge Input, the Judge Output, the main Solving Program, another solution, and another.

[spoiler]
We’ll frame this as a Max Flow problem, but with a twist. We’ll start with a brief discussion of Max Flow problems.

Consider a directional, weighted graph that has a special node called the ‘Source’, and another called the ‘Sink’. Consider the weights to be a ‘capacity’. Think of each edge like a one-way pipe, and the ‘capacity’ is the most stuff you can push through that pipe. (The internet is a series of tubes, right?) Well, the question is… How much stuff can you push from the Source to the Sink, given the limited capacities of all the edges?

The solution technique for a Max Flow problem is called Ford-Fulkerson, and I’ll only give a brief outline of it here.

First, for every edge A⇒B, create a dual edge, B⇒A, which starts with 0 capacity. The way to think of A⇒B and its capacity is: How much capacity is available to use. The way to think of B⇒A and its capacity is: How much capacity has been used, that I could give back if I had to. That’s why B⇒A starts out as 0 – because, at the beginning of the algorithm, you haven’t done anything, so you haven’t used any capacity.

Now, find a path from the Source to the Sink, only traversing edges that have some capacity (that is, capacity>0), and don’t hit any node more than once. You can find this path any way you like, but Breadth-First Search has become the standard.

When you’ve got a path, go back over the edges on the path, and find the one with the smallest capacity. That’s the most stuff you can push through that path, right? That’s the weakest link. Then, go back over the path again, and move that amount of capacity from each edge to its dual (that is, subtract it from each edge, add it to each edge’s dual).

Keep doing this (finding paths, finding the min capacity, moving that capacity from each edge to its dual) until you can’t find a path with >0 capacity. Then, you’re done! The total amount of capacity that you moved over all the paths you found is the Max Flow!

OK, so how do we see Museum Guards as a Max Flow problem? Well, the ‘stuff’ we’ll flow through the system is guard-periods. Build two kinds of nodes, for guards, and for time periods. Link the Source to each guard, with the capacity being the number of time periods that guard is able to work. Link a guard to a time period if the guard is willing to work that time period, with capacity 1. Finally, link the time periods to the sink. What should the capacity for those edges be? Well, that’s tough. We could set them all to n, and see how many guard-periods flow through – but we have no way of forcing the guard-periods to be balanced over the time periods. Some periods could be over-represented, and some under-represented. The result wouldn’t be meaningful. Hmmm….

Consider this: If we set the capacity of each of those links to some value x, 0≤x≤n, and we get a total flow of x*48 (48=number of 30 minute periods in a day), then we know we can cover all time periods with x guards. The only way to geta total flow of x*48 is to get a full x from each of the 48 time periods. We can’t get any more from one time period (and less from another), because we’ve set the max capacity from each time period to the sink to x. That’s our hook. We just have to do repeated Ford-Fulkersons to find the largest value of x which leads to success.
[/spoiler]

This one was just Math. Some teams solved this very quickly, others struggled with it. It was still one of the 4 most solved problems. There were several ways to approach it, which you’ll see in the spoiler.

Check out the Judge Input, the Judge Output, the main Solving Program, another solution, and another, and another, and one in C++.

[spoiler]
I’ll talk about three different solutions, but all of them have one thing in common. They all express points G and H, (and, more specifically, their coordinates Gx, Gy, Hx and Hy) parametrically in terms of a parameter t. This parameter represents how far along ray AC point H is. If t=0, then H is right at A. If t=1, then H is right at C. If 0<t<1, H is between A and C. If t>1, then H is further away from A than C is. Once we know t, we can figure out all the coordinates like this:

Hx = Ax + t*(Cx-Ax)
Hy = Ay + t*(Cy-Ay)
Gx = Bx + t*(Cx-Ax)
Gy = By + t*(Cy-Ay)

The first solution, in euclid.java, is a closed-form solution using more trig than anything else. It uses Heron’s formula to get the area of triangle DEF. It then uses the Law of Cosines to get the cosine of angle CAB. Using the distance of line segment AB (we’ll notate that |AB|), and our target area, we can compute the height of the desired parallelogram as area/|AB|. Since we know the cosine of CAB, we can easily compute the sine, and then use the Law of Sines to get the distance we need along ray AC. Then, t = distance / |AC|. The rest is as above.

The second solution, in euclid_binary.java, uses an age-old trick to get the area of any polygon. For every edge (x1,y1) to (x2,y2), add up (y2+y1)*(x2-x1). The area of the polygon is one half of the absolute value of that. Or,

area = 0.5*|∑(y2+y1)*(x2-x1)|

It uses that trick to get the area of triangle DEF. It then uses that trick to get the area of a parallelogram given parameter t, and uses Binary Search to nail down the correct value of t.

The third solution, in euclid_chinmay.java, uses the fact that the magnitude of the cross product of two vectors (with the same base) gives the area of the paralellogram defined by those two vectors. Also, half of that would be the area of the triangle defined by those two vectors. So, the area of triangle DEF is 0.5*|DExDF|. The area of a parallelogram defined by CAB is |ACxAB|. Then, just let t = 0.5*|DExDF| / |ACxAB|, and we have our answer. This works because the area of the parallelogram we seek will be linearly related to the distance that H is from A along AC.

The other solutions, euclidYiu.java and euclid.cpp, use various combinations of these techniques.
[/spoiler]

This problem had a fairly standard solution, but there was some tricky bookkeeping, which is probably why so few teams solved it. It particular, there were two issues that caught teams.

First, a lot of teams didn’t reset the board correctly when moving pieces. For example, suppose that both pieces A and B can move. Some teams wrote programs that would move piece A all the ways it could move, but would forget to put it back where it started before trying to move piece B.

The other catch was a little more tricky. A lot of teams wrote code that checked to see if the special piece could be moved all the way to the right. They figured that if you could move it there, you could just keep moving it and slide it out. And, most of the time, they would be right – but what if the special piece starts out all the way on the right side of the board? A lot of teams would answer 0 – that is, 0 moves. That’s incorrect. It always takes at least 1 move to remove the special piece.

Check out the Judge Input, the Judge Output, the main Solving Program, another solution, and another.

Join me in the spoiler for an outline of a solution.
[spoiler]
It’s just a breadth-first search. Despite the small size of the board and the limitations on how pieces move, the search space can still get quite large, so if you tried to use Depth-First Search (that is, you tried to solve it recursively) you probably ran out of time.

Create a queue of states. Each state has a board, and a number of moves. Start by putting a state on the queue that has the starting position, with 0 moves.

Each time you take a state off of the queue, check to see if the special piece is all the way to the right. If so, remember the number of moves, and exit the loop. Otherwise, generate all possible boards that can be attained in 1 move. For each, check to see if it’s been seen before, and if not, put it on the queue with a number of moves equal to this state’s number of moves plus one.

When you’re done, output the number of moves remembered, unless it’s 0, in which case output 1, or if you emptied the queue without reaching a solved state, output -1.

Sounds simple in paragraph form, but it’s not necessarily easy to generate all of the possible moves – remember, a lot of teams didn’t reset the board correctly. Also, remembering previously seen board positions is important, otherwise you’ll run out of time and memory.
[/spoiler]